Questão do MIT Sobre Triângulo Retângulo

O canal MindYourDecisions propõe desafios matemáticos interessantes. Eles compartilharam uma questão de admissão do MIT (Massachusetts Institute of Technology) proposta em 1869:

A perpendicular traçada do vértice de um triângulo retângulo até a hipotenusa divide-a em dois segmentos de 9 e 16 respectivamente. Encontre o comprimento da perpendicular e os dois catetos do triângulo.

A resolução deles, que está no vídeo do canal, usa semelhança de triângulos. Eu cheguei à solução usando só álgebra, mas primeiro desenhei o triângulo descrito para poder visualizar o problema:

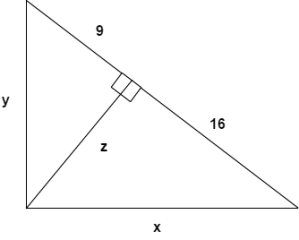
Figura 1 – Um triângulo retângulo formado por dois outros triângulos retângulos

“x” e “y” são os catetos e “z” é a perpendicular como foi descrita. Da figura, extraí as seguintes relações:

(1) y² = 625 – x²
(2) z² = x² – 256
(3) z² = y² – 81

Substituindo (2) em (3) com o objetivo de tirar a dependência de “z”:

x² – 256 = y² – 81
(4) y² = x² – 175

Substituindo (4) em (1) para descobrir o valor de “x”:

x² – 175 = 625 – x²
2x² = 800
(5) x = 20

Substituindo (5) em (1) para descobrir o valor de “y”:

y² = 625 – 400
y = 15

Por fim, basta aplicar Pitágoras em um dos dois triângulos retângulos ou fazer as substituições diretamente em qualquer uma das três equações que trabalhamos em função de “x”, “y” e “z” para deduzir o valor de “z”, que é a perpendicular:

z² = 400 – 256
z = 12

Solução

Das relações algébricas, concluímos que o cateto do triângulo maior (hipotenusa valendo 16) tem comprimento 20, o cateto do triângulo menor (hipotenusa valendo 9) tem comprimento 15 e o comprimento da perpendicular vale 12.